Simple linear regression analysis is used to predict the values of one variable (dependent variable - X) based on the values of one other variable (independent variable - Y). In simple linear regression analysis, relationship between two variables is represented by the straight line (prediction line) fitted (Y = aX + b) to the scatter plot of those variables.
First, lets start by defining our working example. Lets assume that we want to examine relationship between the store size (in thousands of square feet) (X variable) and its annual sales (in million of dollars) (Y variable). We have sample of 14 stores, and data about them:
X= [1.7 1.6 2.8 5.6 1.3 2.2 1.3 1.1 3.2 1.5 5.2 4.6 5.8 3.0];
Y= [3.7 3.9 6.7 9.5 3.4 5.6 3.7 2.7 5.5 2.9 10.7 7.6 11.8 4.1];
Determining prediction line (Y=aX+b)Prediction line (Y = aX + b) where: a is slope of the fitted line, and b is intercept of the line with Y axis. To determine those parameters we can use Matlab/Octave code:
p=polyfit(X,Y,1);
a=p(1); %slop
b=p(2); %icept
In our case a=1.67 and b=0.9645; hence the line is: Y = 1.67X + 0.9645.
What does it mean? The slop means that for each increase of 1 unit in X, the mean value of Y is estimated to increase by 1.67 units. In our case it means that if size of store increases by 1 thousands square feet, the mean annual sales is estimated to increase by 1.67 millions of dollars. On the other hand, the intercept represents the mean value of Y when X equals 0. In our case intercept has no practical meaning because size of store cannot be 0.
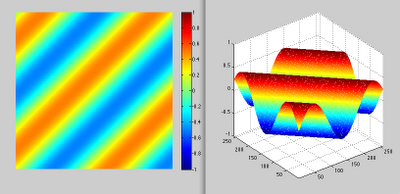
Scatter diagram and fitted regression line are show below:
Standard error of the estimate - SyxPrediction using simple regression line is not perfect; hence, statistic that measure the variability of the actual Y values from the predicted Y values must be developed, in the same way as standard deviation was developed to measure the variability of value around the mean. The standard deviation around the prediction line is called standard error of the estimate - Syx.
Calculation of Syx in Matlab/Octave is:
x=X';y=Y'; %from row vector to column vector.
Sxx=sum((x-mean(x)).^2);
Syy=sum((y-mean(y)).^2);
Sxy=sum((x-mean(x)).*(y-mean(y)));
SSE=Syy-a*Sxy;
S2yx=SSE/(n-2);
%Standard error of estimate:
Syx=sqrt(SSE/(n-2));
In our case we get Syx = 0.9664. The standard error of the estimate is measured in the same units as the dependent variable (Y). In our case defendant variable Y is Annual sales, and our standard error of the estimate is equal to 0.9664 millions of dollars. We can express this value on the scatter plot as below:
Test whether there is a significant linear relationshipIn this section we want to test if there exist a significant (with confidence of 95%; hence, alpha=0.05) linear relationship between X and Y. To do this we can perform t-test for the slop. We do this by stating null and alternative hypothesis as fallows:H0 : A = 0 (There is no linear relationship)
H1 : A = 0 (There is a linear relationship) where A is the slop of the relationship in the population of X and Y. I remained that we have only sample of size 14 from the population. We perform regression analysis on the sample trying to infer relationship in the populations X and Y.
The t statistics equals:
.
We calculate t and P-value and check whether P-value>alpha=0.05; hence, whether we can reject or not our null hypothesis.
%we use date from the earlier code above
Sb=sqrt(S2yx/Sxx);
A=0;
t=(a-A)/Sb;
Pvalue=2*(1-tcdf(abs(t),n-2));
% in older Octave (2.1) use t_cdf!!!
hence t=10.64 and
P-value=1.8227e-07 lower than alpha=0.05 so we reject null hypothesis and conclude that for 95% there is significant linear relationship between mean annual sales and the size of the store.
The confidence interval estimateRegression analysis can be used to predict values of Y based on X. In our case we want to be able to predict the annual sales based on the size of the store. The simplest way to do it, just just point estimate using our line equation Yy = a*Xx + b = 1.67Xx + 0.9645, where Yy is our prediction and Xx is the value of X that we make prediction for. For example, if one asks what is estimated mean annual sales for the store of size 4000 square feet ( Xx=4.0), we calculate
Yy = 1.67*4.0 + 0.9645 = 7.644
Hence, the predicted mean annual sales for the store of size of 4000 square fit
is 7.644 million dollars.
This kind of prediction is called point rediction, and we know that our regression line is not perfect due to standard error of the estimate (Syx). We would prefer to be more statistically correct; hence, we should create confidence interval for our predictions.
Confidence interval estimate for the mean of Y:
Xx=4.0; %predict Y for X=4.
Yy=b+a.*(Xx); %Y predicted from regression line.
SSX=sum((X-mean(X)).^2);
h=1/n + ((Xx-mean(X)).^2)/SSX;
tn2= tinv(1-alpha/2,n-2); %tn-2 - t critical
interval=tn2.*Syx.*sqrt(h);
hence the interval is 0.673.
For example if we want to know the confidence interval of the mean annual sales for the store of size 4.000 square feet ( Xx=4.0), after calculations we get: 7.644 ± 0.673. In other words the mean annual sales are between 6.971 and 8.317 (million of
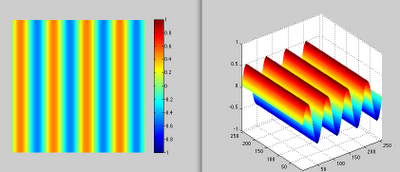
dollars) for the population of stores with 4000 square feet. If we calculate interval for all the X values in our sample, we can show this interval graphically:
For now that is everything what I have to say about this topic; however, this topic is much more longer and complex. But for most situations, it is a good start.
At this point, I had three possibilities:
I wanted to see what would happen if I had performed 'discard current snapshot and state' or 'revert to current snapshot'. Remember that in point 7 above, I removed all my folders, therefore Current State (changed) refers to the guest OS without the folders (i.e. without made_before_a, made_before_b and made_before_c).
After starting my guest OA I had only folders made_before_a and made_before_b! 
This option removes the snapshots but not the current state. In other words, I could remove all my snapshots (named a,b, and c) and I was left only with my current state (i.e. no folders)!
