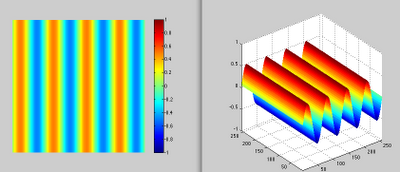
2-D sinusoidal surface is just an sinus function in 2D domain. On the other words, it is image of two-dimensional function sin.
function I=sinSurf(varargin)
%create sinusoidal 2D function (image)
%INPUT
% - theta - angle in radians (default pi/2)
% - lambda - frequency (default 0.5)
% - Isize - output image size (default 256);
% - delta - phase (default 0.0);
%OUTPUT
% - I - double matrix double (-1..1) of sinusoidal function
theta=pi/2;
Isize = 256;
mag=0.5;
lambda=0.5;
delta=0;
if nargin >= 1
theta=varargin{1};
end
if nargin>=2
lambda=varargin{2};
end
if nargin>=3
Isize=varargin{3};
end
if nargin>=4
delta=varargin{4};
end
I=zeros(Isize,Isize);
cosa=cos(theta);
sina=sin(theta);
for x=1:Isize
for y=1:Isize
xprime = (x*cosa+y*sina)/Isize;
valu = mag*sin(2*pi*(xprime/lambda)-delta);
I(x,y)=valu;
end
endBelow some examples:
a) For: theta=pi/2;
s=sinSurf();
imshow(s,[-1 1]);colormap(jet);colorbar;
figure, mesh(s); axis([1 256 1 256 -1 1]); axis square;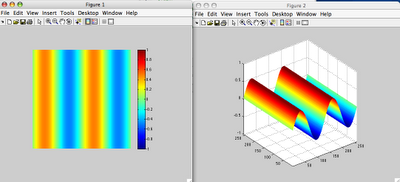
b) For: theta=pi/4;
s=sinSurf(pi/4);
imshow(s,[-1 1]);colormap(jet);colorbar;
figure, mesh(s); axis([1 256 1 256 -1 1]); axis square;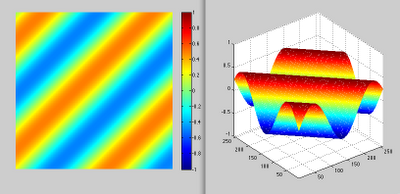
c) For: theta=pi/2; lambda=0.25;
s=sinSurf(pi/2,0.25);
imshow(s,[-1 1]);colormap(jet);colorbar;
figure, mesh(s); axis([1 256 1 256 -1 1]); axis square;