Matlab: making Bland and Altman plots

To do the Bland and Altman plot, we have to compute the differences between the instruments and the mean of both instruments for all the paired values.

For instanceA=[749 583 740 235 735 971 867 86 366 369]
B=[685 598 789 368 206 87 772 206 388 552]
blandAltmanPlot(A,B);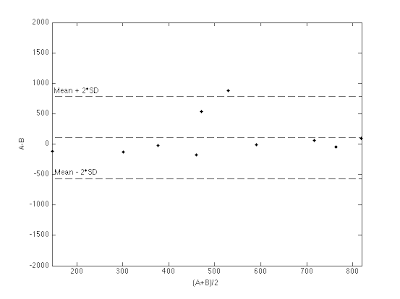


function blandAltmanPlot(A,B)
%reference: Y H Chan, Biostatistics 104:
%Correlational Analysis,
%Singapore Med J 2003 Vol 44(12) : 614-619

meanAB=(A+B)./2;
difff=A-B;
meanDiff=mean(difff);
stdDiff=std(difff);

meanp2D=meanDiff+2*stdDiff;
meanm2D=meanDiff-2*stdDiff;
n=length(difff);
minD=min(meanAB)-0.1;
maxD=max(meanAB)+0.1;

figure;
plot(meanAB,difff,'.k')
hold on;
plot([minD; maxD],ones(1,2)*meanp2D,'--k');
text(minD+0.01,meanp2D+0.01,'Mean + 2*SD');
hold on;
plot([minD; maxD],ones(1,2)*meanm2D,'--k');
text(minD+0.01,meanm2D+0.01,'Mean - 2*SD');
hold on;
plot([minD; maxD],ones(1,2)*meanDiff,'--k');
xlim([minD maxD]);
xlabel('(A+B)/2');
ylabel('A-B');

The excel spreadsheet with the example of Bland and Altman plots is here. These two programs calculated the same statistics.