The solution to a system of two, first order linear differential equations is given by:

To draw this solution one can use the code for Matlab or Octave 3 provided below:

function plotDiff2D() %p. 351, eg. 1 t=[-2:0.1:2]; cT=[-2:.5:2]; for c1=cT for c2=cT x1=c1*exp(3*t)+c2*exp(-t); x2=c1*2*exp(3*t)-2*c2*exp(-t); lineS='b-'; if c1==0 || c2==0, lineS='r-'; end hold on; plot3(x1,x2,t,lineS); end end limm=6 xlim([-limm limm]);ylim([-limm limm]); %axis square xlabel('x1'); ylabel('x2'); zlabel('t'); grid on;

And this script produces graphs of solution in 2D (x1,x2) and 3D (x1,x2,t):

So it is seen from these graphs that solutions of systems of two first order differential equations are very interesting, and not necessarily easy to interpret.

Octave 3: first impression

Octave 3 is out for few weeks now. I have chanced Windows binary. First impression is very positive. Installation went smooth, Octave 3 has now its own console and editor, similar to these in Matlab. 2D and 3D plotting is working:

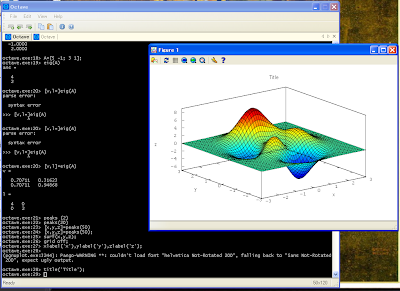Whats more, the problems with eigenvalues that I had with Python (see this post) does not exist in Octave 3. I have to say, that for now I have been working only with eigenvalues, inverse matrices, and multiplication of matrices. But I am encourge to use Octave 3 for longer, to other tasks, and we will see what will happen.

Update:
I found problem with 3D plots. When you draw such plot, often the plot window freezes. As a result is not possible to rotate, zoom or do any operations on the figure. Its very annoying. I use gnuplot as plot engine. I think I will try to use the other one. During installation of the Octave 3 on Windows in one point the user is asked to choose an engine plot. I should try the second one, and we will see what will happen.

Python: eigenvalues with Scipy and Sympy

Eigenvalues and eigenvectors are important in systems of differential equations. To speed up my analysis I decided to use some numerical package for getting eigenvalues form square matrices. I found two numerical packages Scipy and Sympy for Python. Both have ability to calculate eigenvalues. But their calculations are not reliable. I present few very simple examples showing how rubbish these packages are.

Lets see what does Python calculate:
Scipy
from scipy import *
from scipy.linalg import *

A=matrix([ [-5,-5,-9],[8,9,18],[-2,-3,-7] ])
print eigvals(A)
# [-0.999989 +1.90461984e-05j -0.999989 -1.90461984e-05j
# -1.00002199 +0.00000000e+00j]

A2=matrix([ [-5,-5,-9],[8,9,18],[-2,-3,-7] ])
print eigvals(A2)
# [-1.+0.j 　　-1.00000005+0.j 　　-0.99999995+0.j]
Sympy
from sympy import *
from sympy.matrices import Matrix
x=Symbol('x')
A=Matrix(( [-5,-5,-9],[8,9,18],[-2,-3,-7] ))
print roots(A.charpoly(x),x)
# Returns error!!!

A2=Matrix(( [-1,-3,-9],[0,5,18],[0,-2,-7] ))
print roots(A2.charpoly(x),x)
# Returns error!!!

Based on these to examples it is clearly seen that these two packaged are unreliable, at least as far as calculation of eigenvalues is considered.

For matrices 2x2 it was noticed that the eigenvalues are correctly calculated both for real and complex values.

For comparison lets check what does Matlab returns:A=[-5,-5,-9;8,9,18;-2,-3,-7]
eig(A)

ans =

-1.0000 + 0.0000i
-1.0000 - 0.0000i
-1.0000

A2=[-5,-5,-9;8,9,18;-2,-3,-7]
eig(A2)

ans =

-1.0000 + 0.0000i
-1.0000 - 0.0000i
-1.0000

So it is seen that Matlab does correctly calculate these eigenvalues.


Even if one manually calculates characteristic polynomial and would like to gets roots of it, I would recommend neither Scipy or Sympy. As an example I calculate roots of the previously obtained characteristic polynomial for matrices A and A2:
import scipy as sc
p=sc.poly1d([-1,-3,-3,-1])
print p= sc.roots(p)
# [-1.0000086 +0.00000000e+00j -0.9999957 +7.44736442e-06j
# -0.9999957 -7.44736442e-06j]
import sympy as sy
x=sy.Symbol('x')
print sy.solve(-x**3-3*x**2-3*x-1==0,x)
#[-1]

As can be seen calculation of roots of polynomials is also not good. In the second case there is one root (-1) instead of three (-1,-1,-1).

For comparison lets check Matlab (or Octave 3):p=[-1,-3,-3,-1]
roots(p)

ans =

-1.0000
-1.0000 + 0.0000i
-1.0000 - 0.0000i


Based on these results it is seen that its better to use Matlab for calculation of eignevalues.

References:
[1] S.I. Grossman, Multivariable calculus, linear algebra and differential equation, Second edition, 1986